[백준][BOJ1967] 트리의 지름

Algorithm/Tree

by bedamino 2021. 6. 23. 23:16

1. 문제 : https://www.acmicpc.net/problem/1967

1967번: 트리의 지름

파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연

www.acmicpc.net

2. 풀이 : DFS

3. 시간복잡도 : O(N)

4. 설명

그림[1]과 같이 트리의 모든 경로들 중에서 가장 긴 경로의 길이를 트리의 지름이라고 한다. 트리의 지름을 기준으로 원을 그리면 그림[2]와 같다.

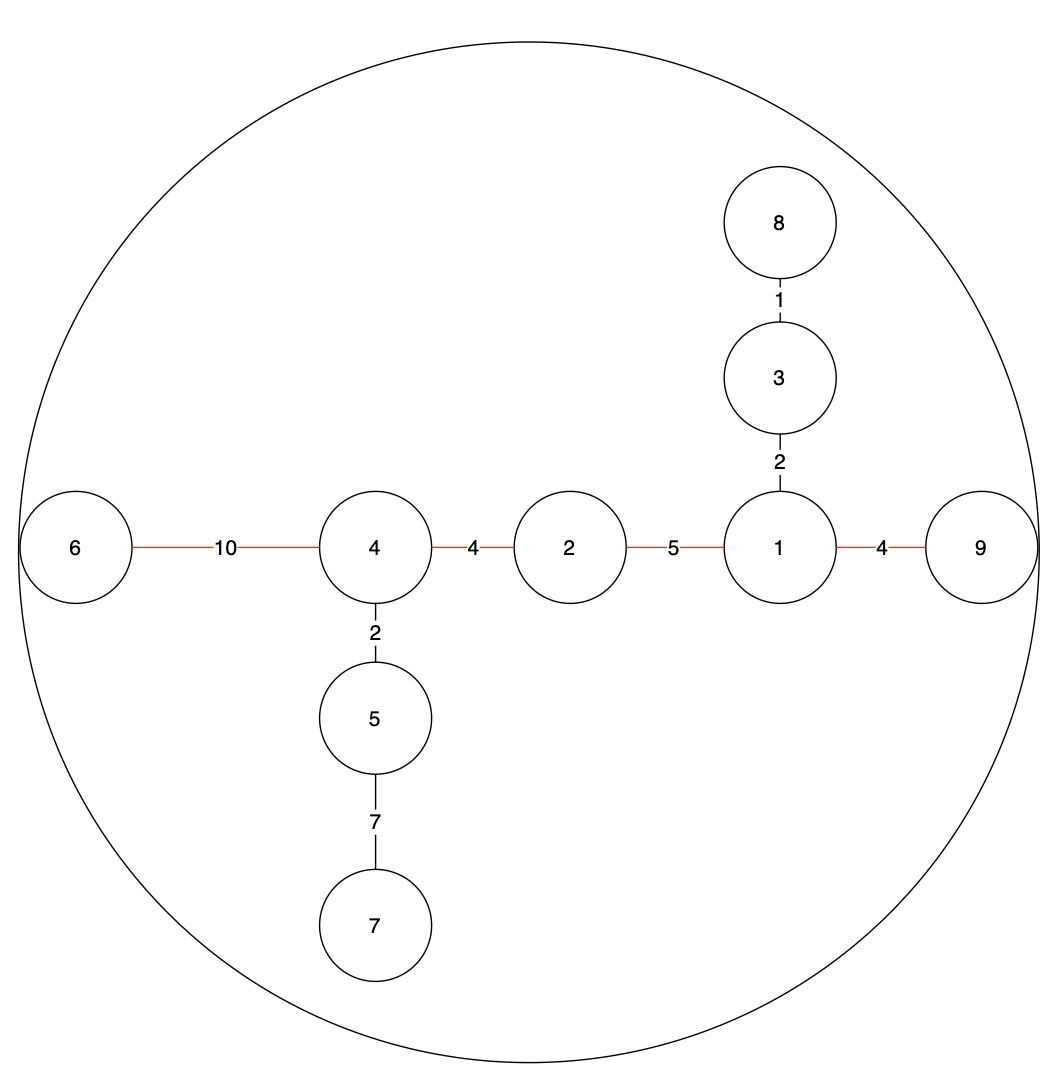
트리의 지름을 구하는 방법은 다음과 같다.

1) 임의의 노드 x에서 가장 먼 거리에 있는 노드 a를 찾는다.

2) 노드 a에서 가장 먼 거리에 있는 노드 b를 찾는다.

3) 트리의 지름은 a와 b를 연결하는 경로이다.

한 점에서 가장 먼 거리에 있는 점은 DFS를 사용하여 찾을 수 있다. 따라서 트리의 지름은 DFS를 2회 수행함으로써 찾을 수 있다.

트리의 지름을 구하는 방법에대한 정당성은 다음 4가지 경우를 증명함으로써 구할 수 있다.

노드 x에서 가장 먼 거리에 있는 노드를 y라고 하고, 노드 a와 b를 연결하는 경로가 트리의 지름일 때,

1. 노드 x가 노드 a이거나 b인 경우

그림[3]과 같이 노드 x가 a인 경우 x에서 가장 먼 거리에 있는 노드가 y가 되기 위해서는 d1과 d2의 값이 같아야 한다. 따라서, 노드 x에서 가장 먼 거리의 노드는 b가 되며, b에서 가장 먼 노드는 a가 되므로 트리의 지름을 구할 수 있다. 노드 x가 b인 경우도 동일하다.

2. 노드 y가 노드 a이거나 b인 경우

1번의 경우와 동일하게 트리의 지름을 구할 수 있다.

3. 노드 x와 y를 연결하는 경로가 노드 a와 b를 연결하는 경로의 일부와 겹치는 경우

그림[4]와 같이 경로 x-y와 경로 a-b의 교차점을 t라고 할 때, 노드 x에서 가장 먼 거리에 있는 노드가 y가 되기 위해서는 d2의 길이가 d3와 d4의 길이 중 긴 경로와 같아야 한다. 따라서, 노드 y는 노드 a 혹은 b여야 한다. 위의 2번의 경우와 동일해지므로 트리의 지름을 구할 수 있다.

4. 노드 x와 y를 연결하는 경로가 노드 a와 b를 연결하는 경로와 겹치지 않는 경우