[백준][BOJ11438] LCA2 (with. BFS)

1. 문제 : https://www.acmicpc.net/problem/11438

11438번: LCA 2

---

2. 풀이 : LCA + BFS

---

3. 시간복잡도 : O(MlogN)

---

4. 설명

문제의 예시를 그림으로 표현하면 그림[1]과 같다.

그림[1]

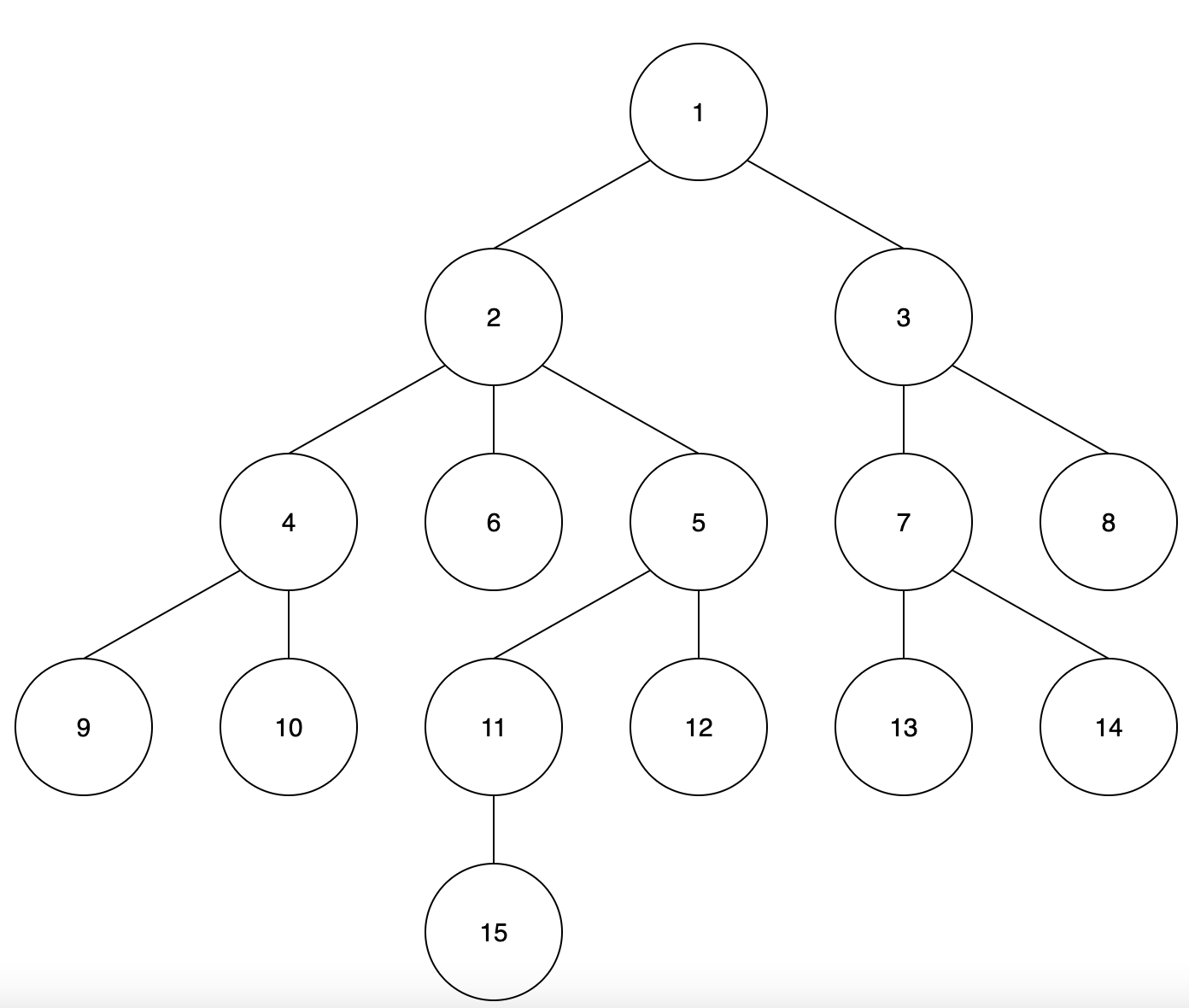
그림[2]와 같이 루트에서부터 BFS를 시작하여 각 노드들의 깊이와 2^0번째 조상, 즉 부모 노드를 확정한다.

그림[2]

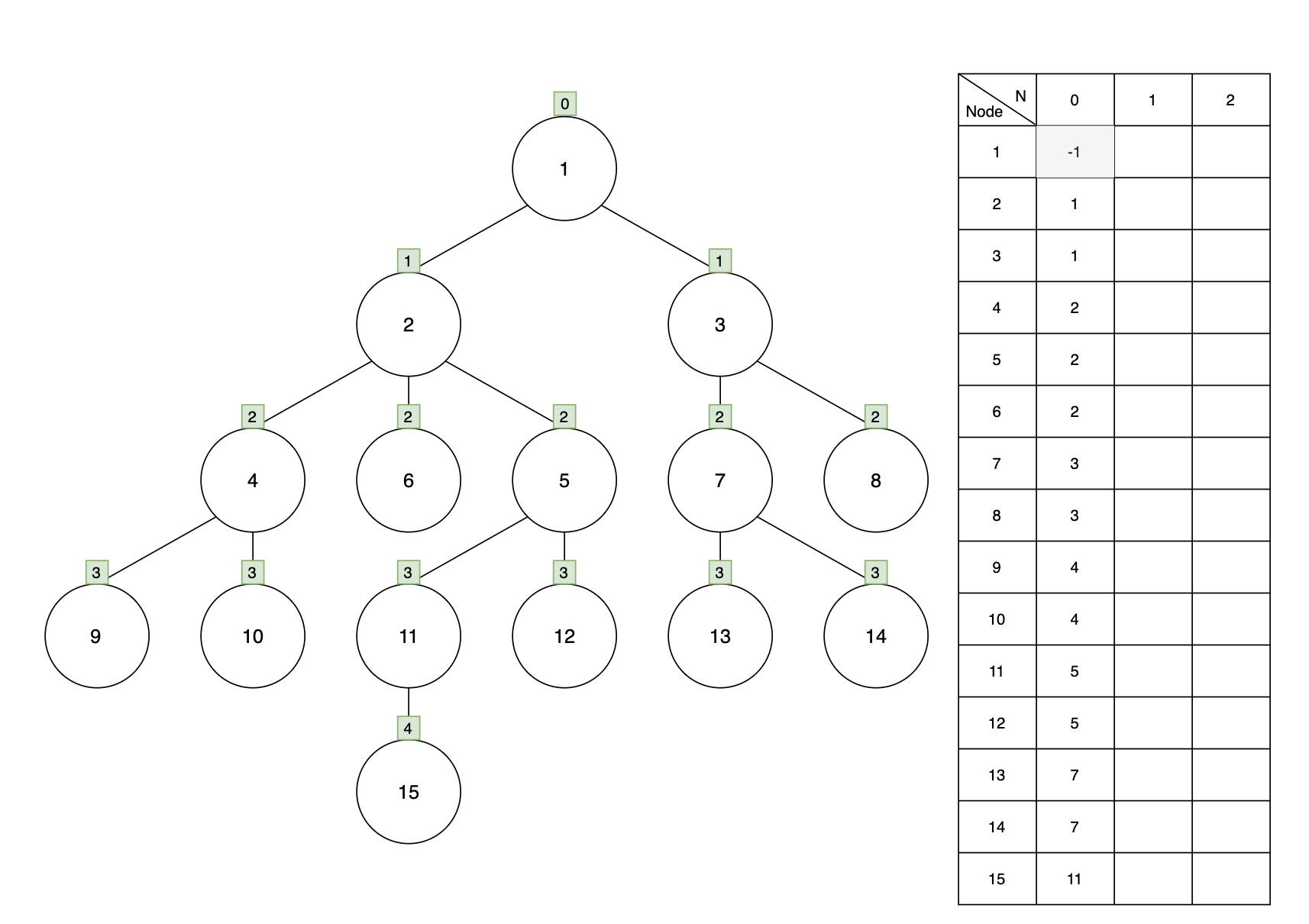
루트 노드의 부모인 '-1'값은 조상이 없음을 의미한다.

그림[3]

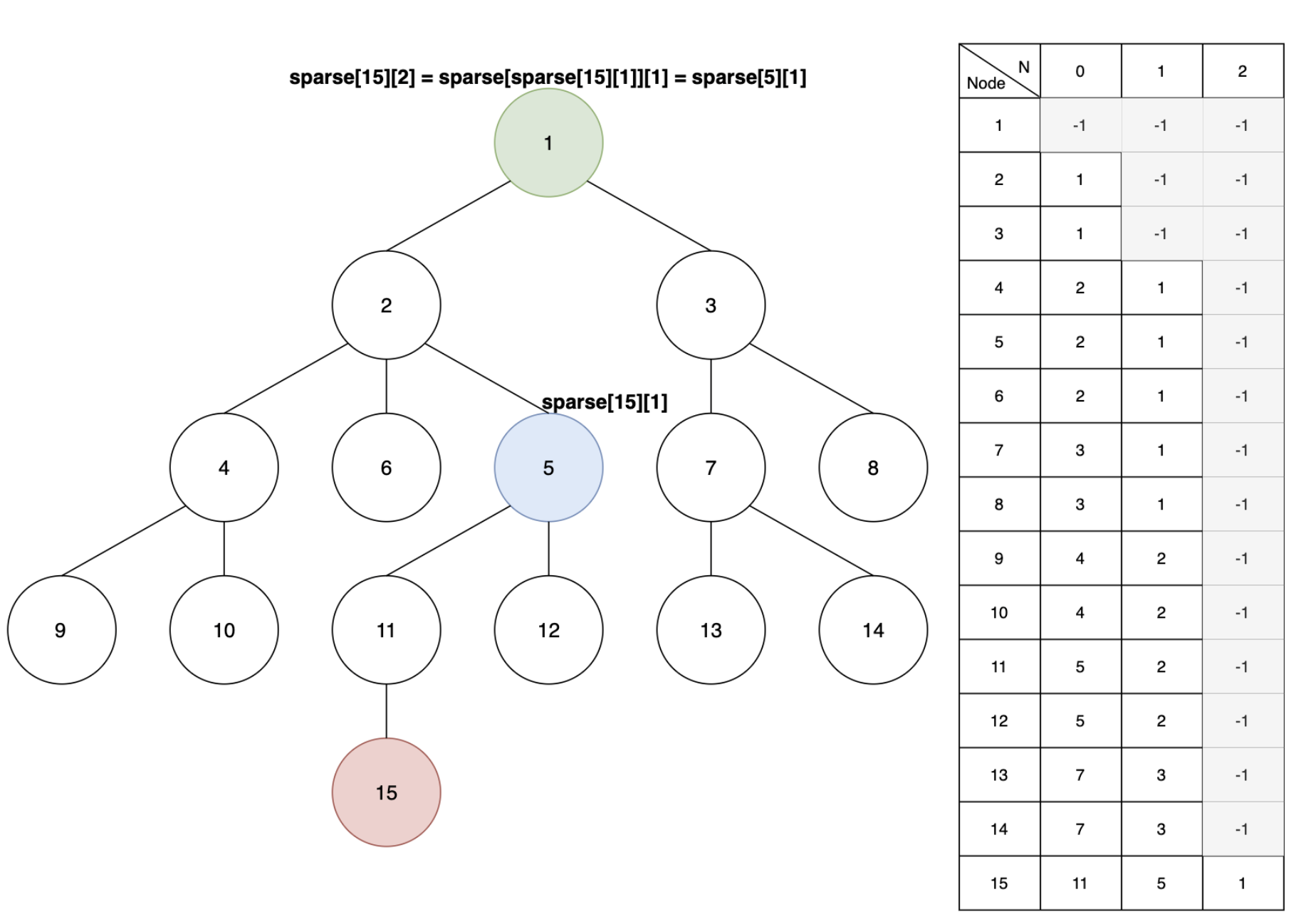
희소 배열을 sparse라고 했을 때, 아래의 식이 성립하며 그림[3]과 같이 각 노드의 나머지 조상 값들을 채워 넣을 수 있다.

sparse[a][n] = sparse[sparse[a][n-1]][n-1]

a와 b의 최소 공통 조상을 찾는 과정은 아래와 같다.

    1. a의 깊이가 b의 깊이보다 깊을 경우, a의 위치를 b의 깊이와 동일한 위치의 노드로 변경한다.

    2-1. b의 깊이와 동일한 위치의 노드로 a를 변경했을 때, a가 b와 같다면 a는 최소 공통 조상이 되며 탐색을 종료한다.

    2-2. a와 b가 다르다면, 깊이가 같아진 a와 b의 위치를 동시에 변경하며 최소 공통 조상의 자식 노드를 탐색한다.

    3. 탐색을 종료하였을 때 a의 부모 노드가 최소 공통 조상이 된다.

15(a)와 14(b)의 최소 공통 조상을 찾는 경우를 예시로 보자.

그림[4]

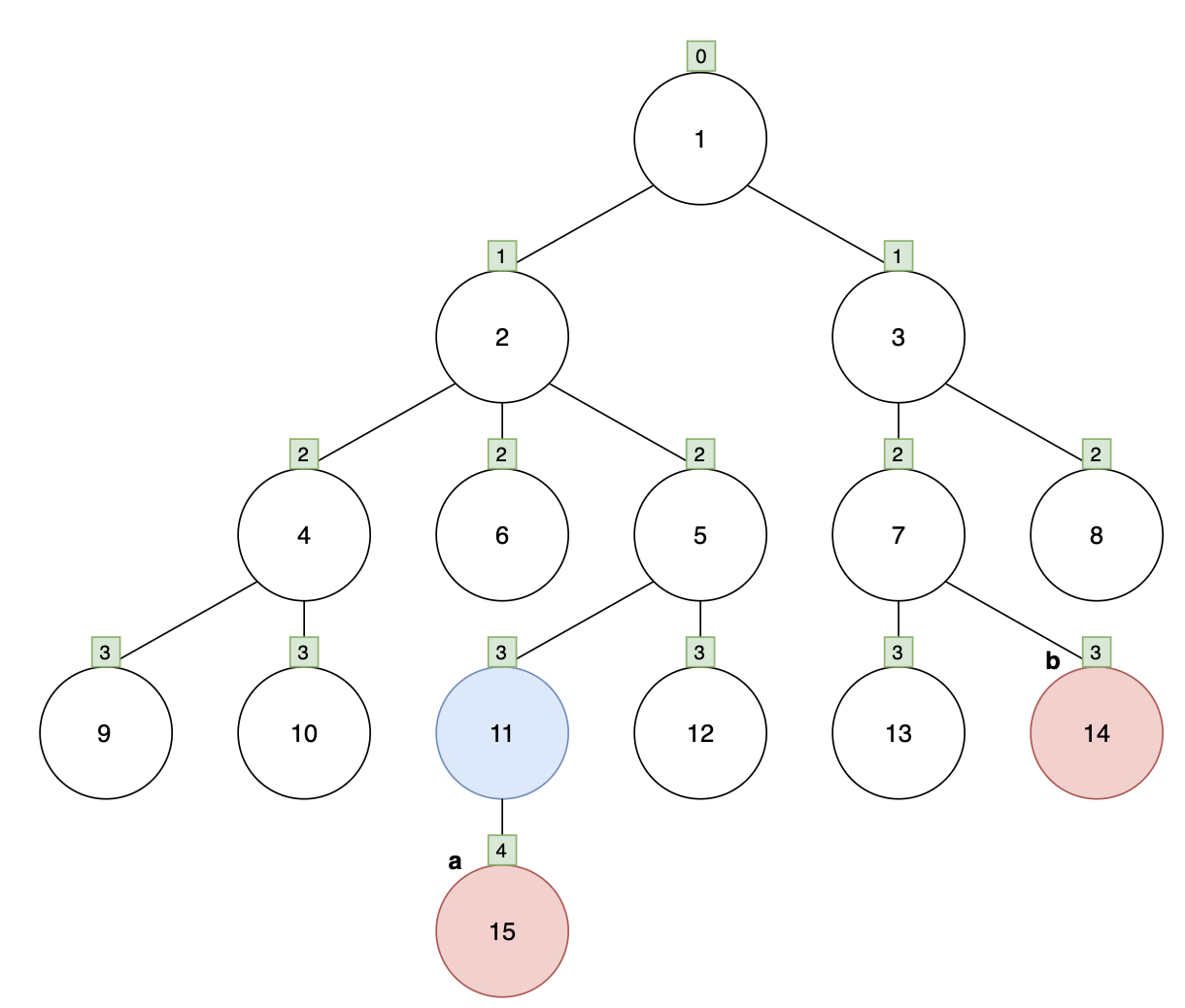
그림[4]에서 15를 14와 동일한 깊이의 노드로 변경하면 11이 된다. 11과 14의 위치를 동시에 변경하여 최소 공통 조상의 자식을 탐색하면 그림[5]와 같다.

그림[5]

탐색을 종료하면 11과 14의 위치는 각각 2와 3으로 변경이 되고, 이때 2와 3은 최소 공통 조상의 자식이므로 2 혹은 3의 부모인 1번 노드가 최소 공통 조상이 된다.

그림[6]

 

---

5. 코드