[백준][BOJ1965] 상자넣기

1. 문제 : https://www.acmicpc.net/problem/1965

1965번: 상자넣기

---

2. 풀이 : Binary Search

---

3. 시간복잡도 : O(NlogN)

---

4. 설명

최장 증가 수열(LIS, Longest Increasing Subsequence) 문제이다.

그림[1]과 같이 LIS를 저장할 배열을 만든다.

그림[1]

상자를 처음부터 하나씩 LIS 배열에 위치를 찾아 넣는다. 위치를 찾을때에는 이분탐색을 사용하며, 동일한 크기의 상자가 들어올 수도 있으므로 lower bound를 사용한다. 크기가 1인 첫번째 상자와 크기가 6인 두번째 상자를 LIS 배열에 위치시키면 그림[2]와 같고, 이 때의 최장 증가 수열의 길이는 2이다.

그림[2]

다음으로 크기가 2인 세번째 상자의 위치는 그림[3]과 같다.

그림[3]

lower bound로 탐색 시, 크기가 2인 상자는 크기가 6인 상자 자리가 된다. 크기가 6인 상자를 크기가 2인 상자로 대체하여도 최장 증가 수열의 길이는 변하지 않는다. 실제로 세번째 상자까지 가능한 최장 증가 수열은 [1, 6]이며 그 길이는 2이다.

이어서, 크기가 5인 네번째 상자의 위치는 그림[4]와 같다.

그림[4]

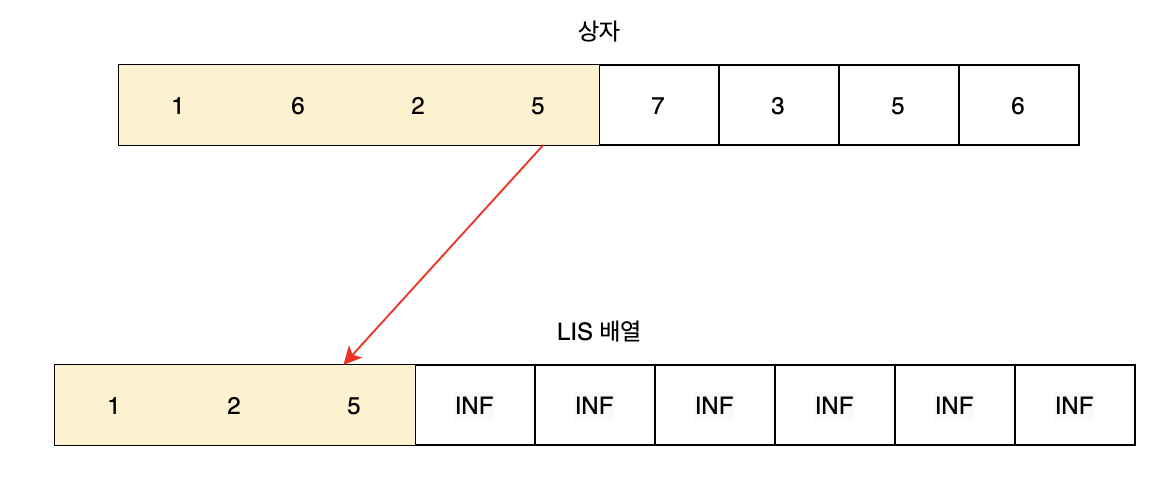
이 때의 최장 증가 수열의 길이는 3이다. 네번째 상자까지 가능한 최장 증가 수열은 [1, 2, 5] 이며 길이는 3임을 알 수 있다.

다섯번째 상자와 여섯번째 상자의 위치는 그림[5]와 같다.

그림[5]

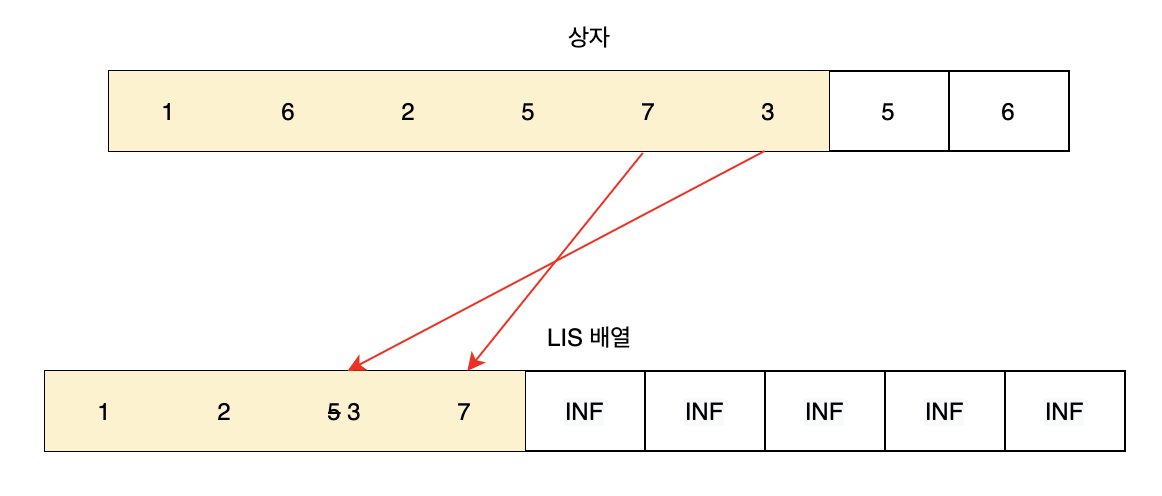
이 때의 최장 증가 수열의 길이는 4이다. 실제로, 여섯번째 상자까지 가능한 최장 증가 수열은 [1, 2, 5, 7] 이며 길이는 4임을 알 수 있다. 그림[5]에서  LIS 배열에 있는 값을 보면 [1, 2, 3, 7] 이지만, 이는 실제로 조합할 수 없는 최장 증가 수열이다. 따라서 LIS 배열에 있는 값들이 실제 최장 증가 수열이 아니라는 것을 알 수 있다. 하지만 그 길이는 유의미하다. 

남은 두 개의 상자를 위치시키면 그림[6]과 같다.

그림[6]

그림[6]에서 상자를 모두 사용했을 때, 최장 증가 수열의 길이는 5임을 알 수 있다.

---

5. 코드